Gleichungen
In[633]:=
gU[k_]:= (xL[k](pu[k]-pu[k-1]) + xL[k+1](pu[k+1]-pu[k]) + xF[k] stabFrom[k] + xT[k] stabTo[k] + kraftU[k]=={0,0});
gO[k_]:= (yL[k](po[k]-po[k-1]) + yL[k+1](po[k+1]-po[k]) + xF[k-1] stabFrom[k-1] + xT[k] stabTo[k] + kraftO[k]=={0,0});
gU[0]= (kAussenP1[p1x,p1y] + xL[1](pu[1]-pu[0])+ xF[0] stabFrom[0] + xT[0] stabTo[0] + kraftU[0]=={0,0});
gO[0]= (kAussenP4[p4x,p4y] + yL[1](po[1]-po[0])+ xT[0] stabTo[0] + kraftU[0]=={0,0});
gU[az+1]= (xL[az+1](pu[az+1]-pu[az]) + xT[az+1] stabTo[az+1] + kraftU[az+1]=={0,0});
gO[az+1]= (yL[az+1](po[az+1]-po[az]) + xT[az+1] stabTo[az+1] + xF[az] stabFrom[az] + kraftO[az+1]=={0,0});
gleichungen=Join[Table[gU[k],{k,1,az}],Table[gO[k],{k,1,az}],{gU[0],gO[0],gU[az+1],gO[az+1]}];
{gleichungen}//Transpose//MatrixForm
Out[640]//MatrixForm=
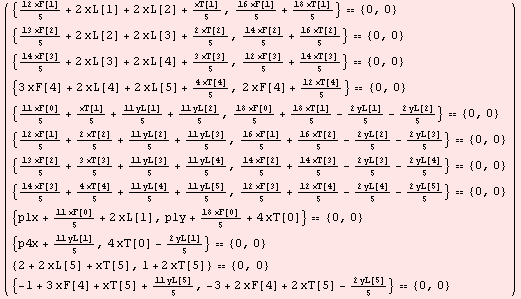
In[641]:=
![varTotal = Join[{p1x, p1y, p4x, p4y}, Table[xL[k], {k, 1, az + 1}], Table[yL[k], {k, 1, az + 1}], Table[xF[k], {k, 0, az + 1}], Table[xT[k], {k, 0, az}] ]](../HTMLFiles/PrototypStatikTragwerke_81.gif)
Out[641]=
![{p1x, p1y, p4x, p4y, xL[1], xL[2], xL[3], xL[4], xL[5], yL[1], yL[2], yL[3], yL[4], yL[5], xF[0], xF[1], xF[2], xF[3], xF[4], xF[5], xT[0], xT[1], xT[2], xT[3], xT[4]}](../HTMLFiles/PrototypStatikTragwerke_82.gif){kind=small}
| Created by Mathematica (December 15, 2006) |  |